A confidence interval (CI) is an interval estimate of a population parameter. Instead of estimating the parameter by a single value, an interval of likely estimates is given.
More precisely a CI for a population parameter is an interval with an associated probability p that is generated from a random sample of an underlying population such that if the sampling was repeated numerous times and the confidence interval recalculated from each sample according to the same method, a proportion p of the confidence intervals would contain the population parameter in question.
Thursday, November 15, 2007
Monday, November 5, 2007
Independency in Probability
The odds against there being a bomb on a plane are a million to one, and against two bombs a million times a million to one. Next time you fly, cut the odds and take a bomb.
— Benny Hill
Two events are independent if the occurrence of one of the events gives us no information about whether or not the other event will occur; that is, the events have no influence on each other.
Independency is a requirement in Central Limit Theorem.
Student t-distribution
Suppose we have a simple random sample of size n drawn from a Normal population with mean  and standard deviation
and standard deviation  . Let
. Let  denote the sample mean and s, the sample standard deviation. Then the quantity
denote the sample mean and s, the sample standard deviation. Then the quantity
 has a t distribution with n-1 degrees of freedom.
has a t distribution with n-1 degrees of freedom.
The t density curves are symmetric and bell-shaped like the normal distribution and have their peak at 0. However, the spread is more than that of the standard normal distribution. This is due to the fact that in formula (1), the denominator is s rather than . Since s is a random quantity varying with various samples, the variability in t is more, resulting in a larger spread.
. Since s is a random quantity varying with various samples, the variability in t is more, resulting in a larger spread.
 has a t distribution with n-1 degrees of freedom.
has a t distribution with n-1 degrees of freedom.The t density curves are symmetric and bell-shaped like the normal distribution and have their peak at 0. However, the spread is more than that of the standard normal distribution. This is due to the fact that in formula (1), the denominator is s rather than
The larger the degrees of freedom, the closer the t-density is to the normal density. This reflects the fact that the standard deviation s approaches ![]() for large sample size n.
for large sample size n.
Articles which reference Student t-distribution:
Saturday, November 3, 2007
Normal Law Distribution
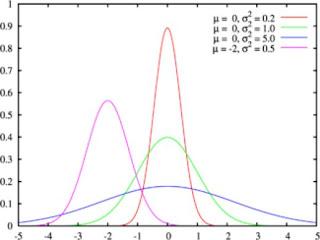
Normal Law Distribution, known popularly as the "Bell Curve" or mathematically as the "Gaussian Law" seems to be a "common sense" law:
It describes mathematically the idea that extremes are rare and elements around averages more and more numerous. So Normal Law could obviously not be a half-circle nor a square but a bell curve.
To characterize the Bell Curve, we only need two parameters: a mean around which most of the population will be found and a standard deviation which impacts the distance between the average and the queues of the extremes.
The existence of Normal Law is based on the Central Limit Theorem.
Articles which reference Normal Law Distribution:
It describes mathematically the idea that extremes are rare and elements around averages more and more numerous. So Normal Law could obviously not be a half-circle nor a square but a bell curve.
To characterize the Bell Curve, we only need two parameters: a mean around which most of the population will be found and a standard deviation which impacts the distance between the average and the queues of the extremes.
The existence of Normal Law is based on the Central Limit Theorem.

Articles which reference Normal Law Distribution:
Central Limit Theorem
The Central Limit Theorem states that if a sum of independent and identically-distributed random variables has a finite variance, then it will be approximately normally distributed and the sampling distribution will have the same mean as the population, but the variance divided by the sample size.
In short the Central Limit Theorem states that the sum of a number of random variables with finite variances will tend to a normal distribution as the number of variables grows.
The smaller variance is intuitivally understandable if one just imagines that one size variation in the sample can compensate another.
In short the Central Limit Theorem states that the sum of a number of random variables with finite variances will tend to a normal distribution as the number of variables grows.
The smaller variance is intuitivally understandable if one just imagines that one size variation in the sample can compensate another.
Subscribe to:
Posts (Atom)